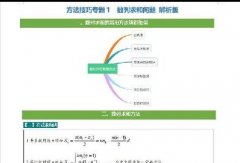
比如，已知物体的初速度V0、加速度a、时间t，怎样求运动的距离S？这个场景非常常见，“苹果下落1秒后落了多远？”就是这类问题（V0=0，a=g=9.8，t=1)。

 

那要怎么做呢？

 

非常简单，要求距离S就得借助关系2（S=（V0+Vt)×t/2），这里V0和t都有了，就差一个Vt，而Vt能够根据关系1（Vt=V0+at）得到。

 

所以，最终的结果就是把关系1的Vt代入关系2，这么我们就能得到了一个不含Vt的关于S的表达式。

 

你亲自去推一下，就会得到这么一个结果：S=V0t+at⊃2;/2。

 

这个式子非常常用，可是我非常不建议你立即把这个公式死记下来，然后用它去套各种题目。

 

因为这个式子的物理意义不是很明显，你能够把这个式子记下来，但很难看清它背后的物理图像。

 

假如你把过多的精力放在记忆这类物理意义不明显的公式上，尽管短时间内可以提升解题速度。但长此过往，会逐渐丧失对物理图景的把握，会认为物理越来越无聊，就是一堆公式游戏，那就完蛋了。

 

物理学是描述自然的，自然就在我们眼前，我们能看到，能感觉到。所以我们用来描述自然界的物理语言，也应该是能看到，能感觉到的。

 

我们学习物理，要尽力看清公式背后的物理图像，假如你认为那些公式非常简单，那物理就会很简单。

 

因此，整篇文章都在告诉你高中物理的框架是什么，怎样看清它的物理图像。我们想告诉你，物理学的每一种想法，每一个公式的来源都是有理有据有节操，合情合理又合法的。

 

关于物体的运动部分，我们只要知道描述物体运动的5个物理量之间有2个意义非常明确的关系式，其它公式都能从这里推出来就完了。

 

5个物理量，2个方程，你想推导不包含哪个物理量的方程，用消元法把它消掉就行了，不用死记它们。我们须要记住的是牛顿力学处理问题的一般方法，以及这背后的物理图像。

 

再回到上面的式子，不包含Vt的公式是这么的：S=V0t+at⊃2;/2。你须要这个公式时，临时推一遍就完了，耽误不了你多少时间。推导次数多了，很快就自然记住了。

 

你因为推导次数过多自然记住的，比死记下来的效果强太多了：第一，你永远不用担忧会忘记公式；第二，作为出发点的那两个关系式的物理意义足够明显，所以你会认为推导结论的物理意义也足够明显；第三，这个过程会锻炼你的逻辑推理能力，喜欢推公式的人，数学、物理都不会差。

 

假如没有理清物理框架，没有看清公式背后的物理图像，只是死死地记住了一堆结论，记住了一堆特定问题的特殊解法，那物理会学得非常痛苦。

 

好，再来试一个，假如把时间t消掉，初速度V0、末速度Vt、加速度a、距离S之间就会有这么一个关系式：Vt⊃2;-V0⊃2;=2aS。相同，别去死记它，别把非常有意思的物理搞成了无聊的字母游戏。

 

本着这类精神，你会发现出题人在物体运动状态这一边能动的手脚也非常有限，无非就是在这几个量之间变来变去。

 

20

 

场景复杂化

 

再回到核心的牛顿第二定律F=ma上来。

 

在这篇文章里，我坚持在牛顿第二定律后面加上了F=ma，假如你能看到这里来，看了这样多遍F=ma，应该形成条件反射了吧？

 

牛顿第二定律F=ma是整个牛顿力学的核心，它把物体的受力状况和运动状况联系在了一起，并且告诉我们物体受力以后要如何运动。

 

围绕它出题，也只能一方面把物体的受力状况复杂化（添加各种各样的力，复杂化受力分析），一方面把物体的运动状况复杂化（V0、Vt、a、t、S五个量颠来倒去的变）。

 

假如还不够复杂，那就增多场景的数量。

 

比如，我让小球从光滑斜面上滚下来，这非常简单。那好，我再增多一个场景：小球滚下来以后再经过一个摩擦力无法忽略的地板，在摩擦力的作用下慢慢减速。

 

还不够复杂？那我再增多一个磁场（电场），让小球滚进磁场（电场）里运动；加一个弹簧，让小球被反弹运动；加一个传送带……