科学讲究以简驭繁,它把个体差异定义为个体对群体平均值的距离:
个体差异=

式中的Xi表示一名个体的一项特质的表现程度,而
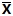
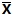
(Xi-
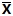
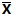
个体差异的离均差定义有这样的好处:
(1)它确立了一个固定的比较点,就是平均值。于是所有的个体都通过与平均值作比较而显出自己的差异来。这样,要了解40名学生在某项特质上的个体差异,只需比较40次就行了。比较的程序简化了,也就更加实用了。
(2)以平均值为比较点,则有大体一半的个体在平均值以上,一半在以下,于是平均值就可以作为最粗大的“质的差异”分界线。这在日常工作中又简化了个体差异的比较,即把个体差异粗分为两类,高于还是低于平均值。于是我们判断任何一个个体,可以先考虑他(她)落在平均值的哪一边。
(3)个体差异的离差定义包容个体差异的“两两间差异”的定义,因为引用式[1]之后,所得的差越大,就表明这一个Xi的这一特质的表现程度越特别,根据它的数值为正还是为负,就可以具体说明为该特质的表现是越充分还是越欠缺、越好还是越糟,从而确定是优先举荐还是重点扶助。
(4)个体差异的离差定义还可以进行数学运算,从而可以更深入地分析考察个体差异,使个体差异的考察超出日常思维的范围而升入科学研究的领域。
 导航
导航

















